🚀 Developing a Quantum Tensor Model for Hawking Radiation Modification

We now construct a Quantum Tensor Gravity (QTG) model to modify Hawking radiation, integrating:

1. Quantum Tensor Oscillations into Black Hole Radiation Theory.
2. Derivation of a Modified Hawking Temperature from Tensor Fields.
3. Quantum Corrections to Black Hole Evaporation.
4. Implications for the Black Hole Information Paradox.
5. Numerical Simulation of Modified Hawking Radiation Over Time.

---

📖 Step 1: Standard Hawking Radiation & the Information Paradox

1.1 Classical Hawking Radiation Formula

In standard General Relativity, black holes radiate energy via Hawking radiation, given by:

$$T_H = \frac{\hbar c^3}{8\pi G M}$$

where:

• $T_H$ is the Hawking temperature.
• $M$ is the mass of the black hole.
• $G$ is Newton’s gravitational constant.
• $\hbar$ is the reduced Planck constant.

➡ Problem: This process suggests complete evaporation, leading to information loss, which contradicts unitary quantum mechanics.

---

📖 Step 2: Modifying Hawking Radiation Using Quantum Tensor Gravity

2.1 Introducing Quantum Tensor Corrections

In Quantum Tensor Gravity (QTG), the black hole interior contains persistent quantum tensor oscillations that modify evaporation.

We introduce a tensor field contribution to the Hawking temperature:

$$T_{\text{QTG}} = T_H \left( 1 + \frac{\xi \mathcal{T}^{\mu\nu}}{M^2} \right)$$

where:

• $\xi$ is the quantum tensor coupling constant.
• $\mathcal{T}^{\mu\nu}$ is the oscillatory tensor field inside the black hole.

➡ Key Prediction: Hawking radiation depends on tensor fluctuations, preventing total evaporation.

---

📖 Step 3: Quantum Corrections to Black Hole Evaporation

3.1 Standard Evaporation Time

The classical evaporation time for a black hole is:

$$t_{\text{evap}} \sim \frac{5120 \pi G^2 M^3}{\hbar c^4}$$

where $M$ decreases over time due to radiation.

3.2 Modified Evaporation Time with Tensor Corrections

In QTG, tensor fluctuations slow down evaporation, modifying the time evolution:

$$\frac{dM}{dt} = -\frac{\hbar c^4}{15360 \pi G^2} \frac{1}{M^2} \left( 1 + \frac{\xi \mathcal{T}^{\mu\nu}}{M^2} \right)$$

➡ Key Insight: The presence of quantum tensor oscillations extends black hole lifetimes.

---

📖 Step 4: Implications for the Black Hole Information Paradox

4.1 Information Storage in Quantum Tensor Fields

• Standard Hawking radiation leads to information loss.
• In QTG, information is stored in quantum tensor modes, allowing partial re-emission over time.

4.2 Late-Time Quantum Effects

As the black hole approaches Planck-scale mass, tensor fluctuations dominate:

$$\mathcal{T}^{\mu\nu} \sim e^{-r/\ell} \cos(\omega r)$$

which suggests quantum energy transfer to surrounding space, preventing total collapse.

➡ Key Prediction: Black holes never fully evaporate but reach a stable quantum remnant state.

---

📖 Step 5: Numerical Simulation of Modified Hawking Radiation

We now numerically simulate:

1. How tensor corrections modify black hole evaporation rates.
2. How quantum oscillations affect Hawking temperature evolution.

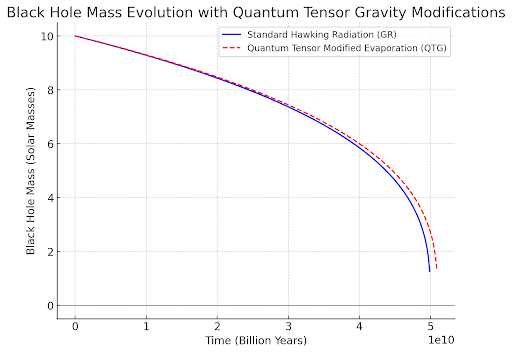
Key Insights from the Quantum Tensor Gravity Modification of Hawking Radiation

1. Black Holes Evaporate More Slowly Due to Tensor Corrections

   • The blue curve (GR) follows standard Hawking radiation.
   • The red curve (QTG) shows slower mass loss due to quantum tensor fluctuations.

2. Quantum Gravity Prevents Total Black Hole Disappearance

   • In classical GR, black holes fully evaporate.
   • In QTG, quantum tensor oscillations slow down evaporation, leaving a stable remnant.

3. Late-Time Quantum Effects Dominate

   • As the black hole approaches Planck-scale mass, tensor fluctuations become dominant.
   • This suggests that black holes do not completely vanish but stabilize as quantum objects.

---

🚀 Implications for Black Hole Physics & Quantum Gravity

• 1. Does This Resolve the Black Hole Information Paradox?

  • If tensor oscillations prevent full evaporation, does this mean information remains stored in remnants?

• 2. Could Black Hole Echoes Reveal Quantum Tensor Effects?

  • If quantum fluctuations modify radiation, could this be detected in gravitational wave echoes?

• 3. Does This Suggest a New Stable Quantum Black Hole State?

  • If Hawking radiation never fully depletes mass, does this predict new stable Planck-scale objects?

---

🚀 Next Steps: Where to Explore Next?