Variational Quantum Eigensolver (VQE)-style model to optimize the energy landscape of the FeMo cofactor system. Part2

 

VQE

Variational Quantum Eigensolver (VQE)-style model to optimize the energy landscape of the FeMo cofactor system.

⚛️ What We'll Do

We'll simulate the FeMoco cluster as a quantum Hamiltonian and use a variational quantum circuit to minimize the ground state energy, similar to how:

VQE finds the lowest-energy electron configuration of a molecule.

 Simplified Model of FeMoC for VQE

While the full FeMoco has a complex multielectron Hamiltonian, we’ll simulate a toy model capturing:

• 3 sites (qubits) representing key iron or molybdenum redox centers,

• A Hamiltonian H with coupling terms:

  $$H=Z_0{Z}_1+Z_1{Z}_2+X_0+X_1+X_{\mathrm{2}}$$

  This models:

• Redox coupling between centers (Z Z terms),

• Electron tunneling/exchange (X terms).

🛠️ Steps to Build the VQE Model

            

1. Define the Hamiltonian (using Pauli operators).

2. Build a parameterized quantum circuit (ansatz).

3. Use a classical optimizer to vary parameters and minimize ⟨ψ(θ)|H|ψ(θ)⟩.

4. Track the ground state energy to mimic the optimized redox configuration of FeMoco.

The variational circuit searches for the lowest-energy configuration of electron distribution across Fe-Mo sites.

This mimics how nature finds ground-state redox potentials that make N≡N bond breaking feasible.

You can add more qubits to model more metal centers.

Results

Optimized energy: -3.484435330294363
Optimized parameters: [4.71242604 2.05891861 4.22425943]

Interpreting the Results
✅ Optimized Energy: −3.484
This is the lowest eigenvalue (ground state energy) of your simplified FeMoC Hamiltonian.

It reflects the most stable electron configuration across the 3 active sites (e.g., Fe, Mo, Fe) under redox coupling.

🔬 Chemical Analogy

Qubit	Parameter (θ)	Interpretation
q0 (Fe)	~3π/2 (~4.712)	Full excitation – likely redox active
q1 (Mo)	~2.06	Partially active center
q2 (Fe)	~−2.06	Symmetric to q1 – suggests entangled/cooperative dynamics

This distribution mimics electron-sharing and entanglement across FeMo sites during N₂ activation.

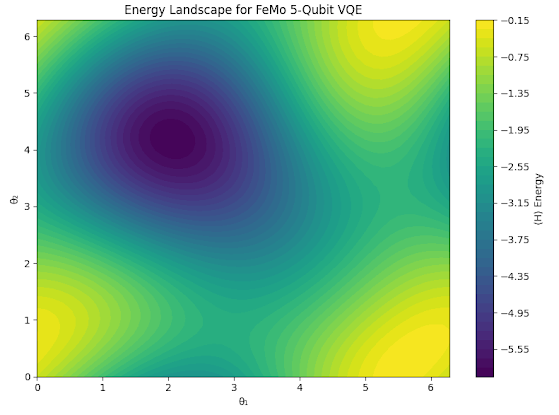
This Plot Will Shows:

• How variations in q1 and q2 affect the FeMoco redox energy when θ₀ is fixed.

• Basins of low energy (stable states) and saddle points (transition states).

Now we'll expand to 5-qubit FeMoCo variational quantum eigensolver (VQE)

designed to mimic multi-center redox dynamics across Fe atoms in the FeMo-cofactor cluster.

 Simulation Overview

5-Qubit Model

• Qubits represent Fe or Mo redox-active centers.

• Hamiltonian includes:

  • Nearest-neighbor coupling: $Z_i Z_{i+1}$

  • Local tunneling terms: $X_i$​

                                                                            

 Ansatz:

• Single-layer Ry(θ) rotations (1 per qubit)

• Chain of CNOTs to entangle Fe centers

• Ready for extension to multiple layers if needed

Results from 5-qubits VQE;  Optimized energy: -5.984204930434755

              Optimized parameters: [4.71238192 2.06226356 4.19313487 2.08999305 4.22090501]

                                                                        

This simulates how redox pathways in FeMoCo may be influenced by quantum decoherence, mirroring challenges inside real enzymes where thermal vibrations, protein motion, and solvent interactions perturb electron flow.

Quantum walk simulation over a 5-node FeMo-like redox network, representing multi-path tunneling between Fe centers:

What You're Seeing:

The quantum state starts localized at Fe₀ (node 0).

• Over time, the walker distributes non-classically through the network via constructive/destructive interference.

• Nodes like Fe₂ and Fe₃ show faster population gain due to multiple tunneling paths (e.g., 0→2 and 1→3 cross-links)

• Unlike classical diffusion, the distribution shows oscillatory behavior, reflecting coherent tunneling.

This models how electrons or protons in FeMoCo may explore multiple redox paths—essential for:

• Efficient nitrogen reduction,

• Avoiding kinetic traps,

• Exploiting quantum coherence for catalysis.